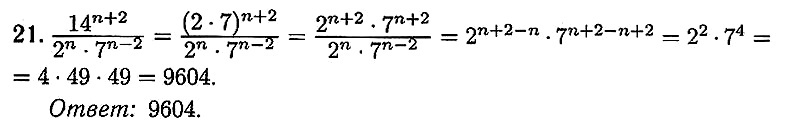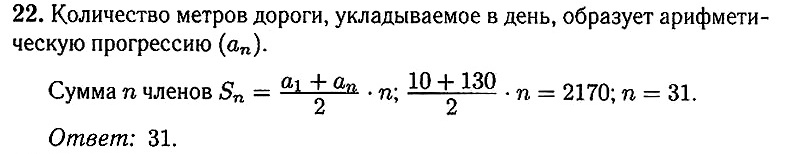ОГЭ Математика. Тренировочный вариант 1

ОГЭ 2020 Математика. Тренировочный вариант № 1 (оффлайн задания) с ответами и решениями. Составлен по проектам демоверсии и спецификации ОГЭ 2020 года (ФИПИ). Посмотреть все варианты тренировочных заданий по математике.

---

 

Математика.
Тренировочный вариант 1

Часть 1

 Прочитайте внимательно текст и выполните задания 1—5. 

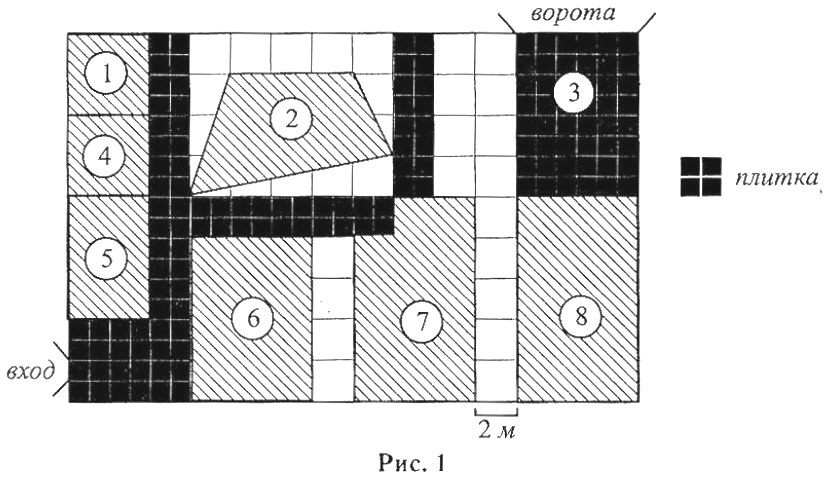
На плане (см. рис. 1) изображён «Живой уголок» городского парка (сторона каждой белой клетки на плане равна 2 м).
Участок имеет прямоугольную форму. Имеются ворота для служебного пользования и вход для посетителей. Рядом с воротами находится площадка для служебного транспорта, а сразу за ней — служебное помещение, в котором размещены склад, администрация и ветеринарный пункт. Напротив входа для посетителей находится уголок домашних животных, а слева от входа — вольер для хищных птиц.
Площадь вольера для хищных птиц равна 24 кв. м. Вольер для косули, отмеченный цифрой 4, находится между вольером для хищных птиц и беседкой для голубей. В глубине участка имеется пруд для водоплавающих птиц. Кроме того, между уголком домашних животных и служебным помещением есть помещение для хищников. Все дорожки на территории «Живого уголка» имеют ширину 2 м и вымощены тротуарной плиткой размером 1 м х 1 м. Стоянка для служебного транспорта вымощена такой же плиткой. Площадь стоянки равна 48 кв. м.
К «Живому уголку» подведено электричество.

1 Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

Ответ:

2 Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось купить, чтобы выложить все дорожки «Живого уголка» и площадку для служебного транспорта?
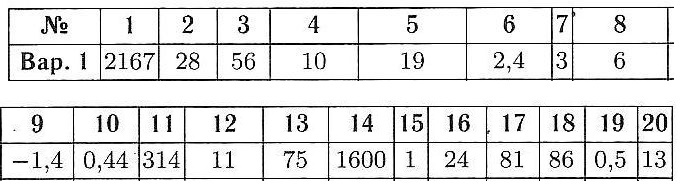
Ответ:

3 Найдите площадь, которую занимает помещение для хищников. Ответ дайте в квадратных метрах.
Ответ:

4 Найдите расстояние от входа для посетителей до пруда (расстояние между двумя ближайшими точками по прямой) в метрах.
Ответ:

5 Администрация «Живого уголка» для того, чтобы поить животных, а также менять воду в пруду и производить уборку, вынуждена использовать 12 м³ привозной воды в неделю, которая обходится в 300 рублей за 1 м³. В настоящее время получено разрешение на бурение скважины прямо на территории «Живого уголка». Разведывательные работы показали, что водоносный слой находится на глубине 25 метров. После консультаций со специалистами стали известны предстоящие расходы.

Через сколько недель после начала эксплуатации затраты на установку и использование скважины окупятся? Считайте, что объём потребляемой воды не изменится. Ответ округлите до целого числа.
Ответ:

6 Найдите значение выражения (4,2 • 2,8)/4,9
Ответ:

7 Одна из точек, отмеченных на координатной прямой (см. рис. 2), соответствует числу √22. Какая это точка?

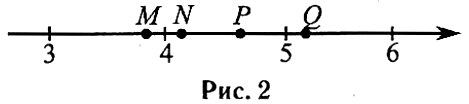
1) М               2) N              3) Р                 4) Q
Ответ:

8 Найдите значение выражения 
Ответ:

9 Решите уравнение 5х + 7 = 0.
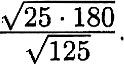
Ответ:

10 Родительский комитет закупил 25 книг для подарков детям, из них 11 со сказками и 14 с рассказами о животных. Подарки распределяются случайным образом. Найдите вероятность того, что Яше достанется книга со сказками.
Ответ:

11 Установите соответствие между графиками функций (см. рис. 3) и формулами, которые их задают.

ГРАФИКИ

ФОРМУЛЫ
1) у = –2х + 1             2) у = –2х – 1            3) у = 2х + 1              4) у = 2х – 1

В таблице под каждой буквой укажите соответствующий номер. Ответ:

А	Б	В
.	.	.

12 Последовательность задана формулой а_n = 52/(n + 6). Сколько членов этой последовательности больше 3?
Ответ:

13 Найдите значение выражения (а — 3)² + 3а(7а + 2) при а = √3.
Ответ:.

14 Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Сколько шагов прошёл человек, если l = 75 см, s = 1,2 км?
Ответ:

15 Решите неравенство 3 — х ≥ 4х + 1.
1) (—оо; 0,4]           2) [0,4;+оо)             3) (—oо; 2,5]               4) [2,5; +oo)
Ответ:

16 В треугольнике АВС угол С равен 90°, АС = 26, tg А = 12/13. Найдите ВС.
Ответ:

17 Периметр квадрата равен 36. Найдите площадь квадрата.
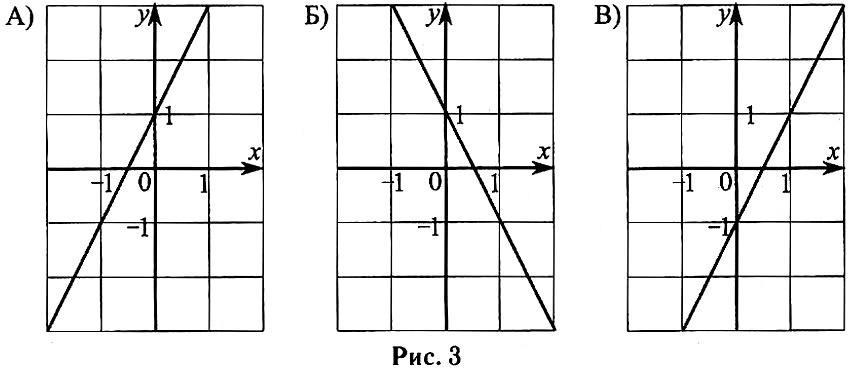
Ответ:

18 Отрезки АВ и CD — диаметры окружности с центром О. Угол ABD равен 47° (см. рис. 4). Найдите угол АОС. Ответ дайте в градусах.
Ответ:

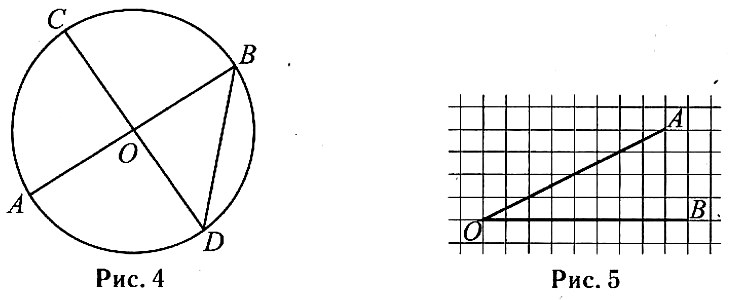19 На клетчатой бумаге с размером клетки 1 x 1 изображён угол (см. рис. 5). Найдите тангенс этого угла.

20 Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Смежные углы равны.
3) Всякий равносторонний треугольник является остроугольным.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ:

 

Часть 2

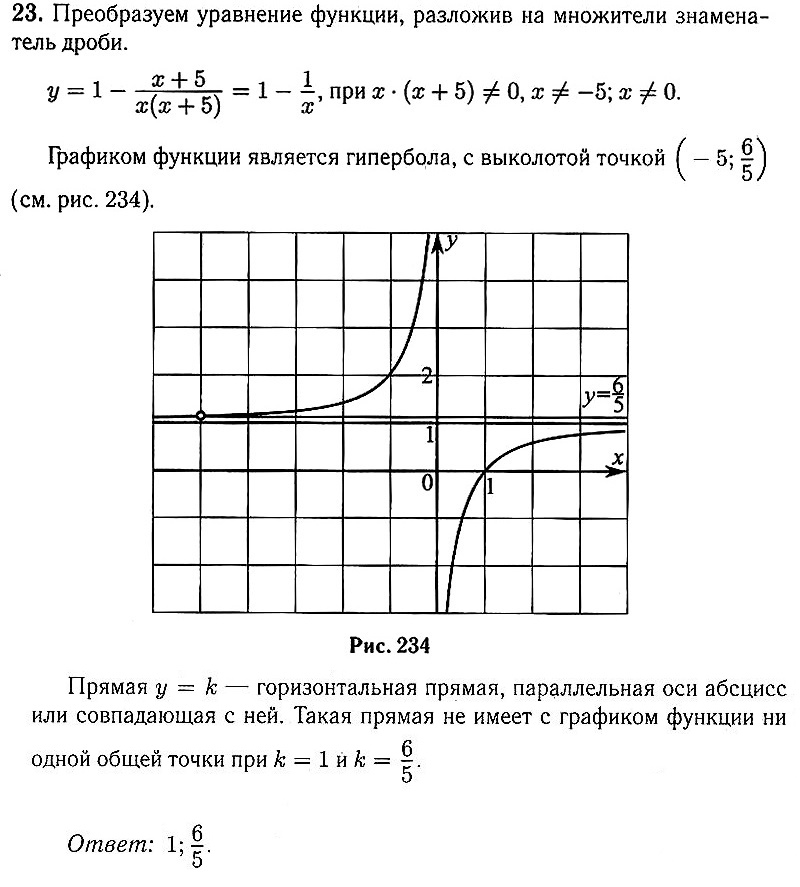
21 Сократите дробь  

22 Рабочие меняют старые рельсы на новые, каждый день укладывая на одно и то же число метров больше, чем в предыдущий день. В первый день заменили 10 м рельсов, а в последний — 130 м. Сколько дней длилась замена рельсов, если общая протяжённость заменённых рельсов составляет 2170 м?

 

23 Постройте график функции  
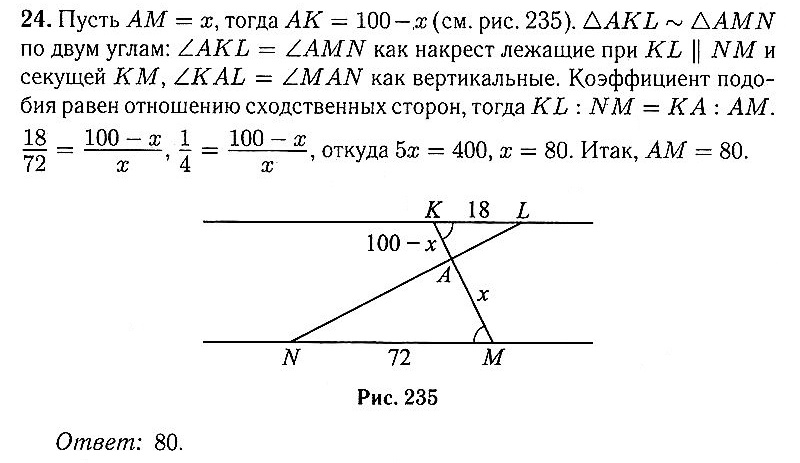
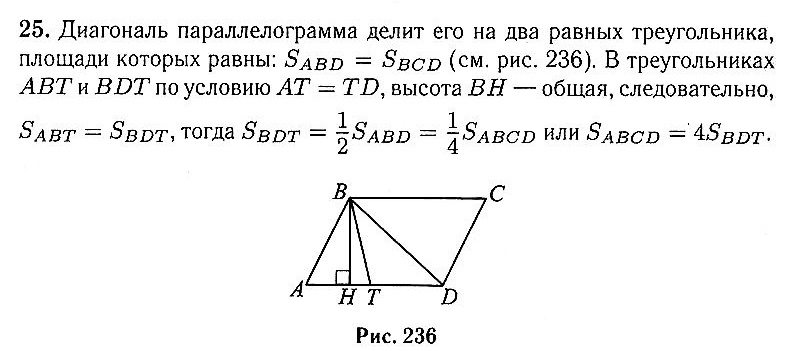
и определите, при каких значениях k прямая у = k не имеет с графиком ни одной общей точки.

24 Отрезки KL и NM лежат на параллельных прямых, а отрезки КМ и LN пересекаются в точке А. Найдите AM, если KL = 18, NM = 72, КМ = 100.

25 В параллелограмме ABCD точка Т — середина стороны AD. Докажите, что площадь параллелограмма ABCD в 4 раза больше площади треугольника BDT.

26 Биссектриса MN треугольника РКМ делит сторону РК на отрезки PN = 20 и NK = 15. Касательная к описанной окружности треугольника РКМ, проходящая через точку М, пересекает прямую РК в точке Т. Найдите МТ.

 

---

ОГЭ 2020 Математика. Тренировочный вариант № 1 (оффлайн задания) с ответами и решениями. Составлен по проектам демоверсии и спецификации ОГЭ 2020 года (ФИПИ).

Посмотреть все варианты тренировочных заданий по математике.