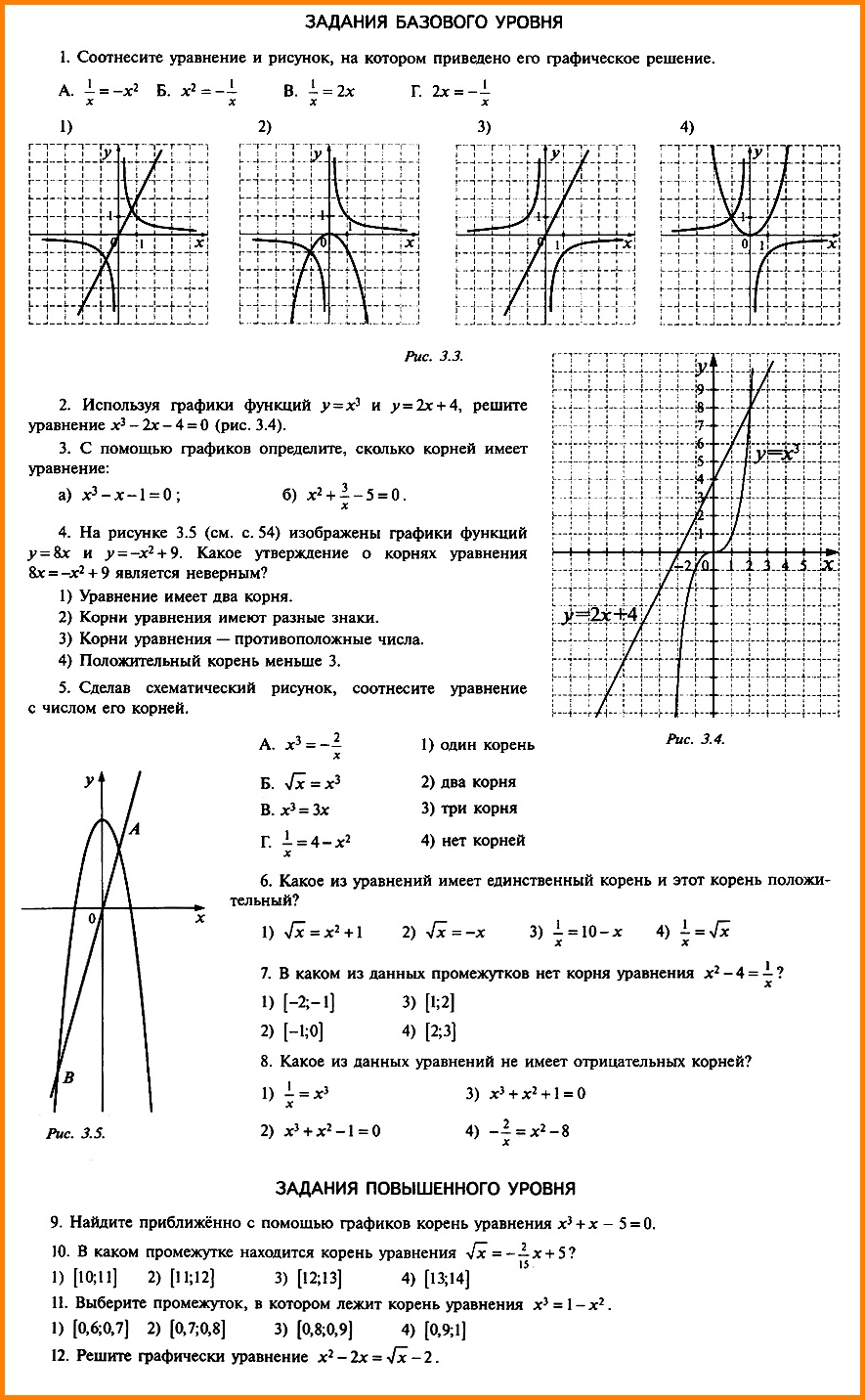
ЗАДАНИЯ БАЗОВОГО УРОВНЯ
1. Прочитайте задачу: Скорость автобуса на 25 км/ч меньше скорости автомобиля. Расстояние от города до посёлка автобус проезжает за 3 ч, а автомобиль — за 2 ч. Каково расстояние между городом и посёлком?
Пусть расстояние между городом и посёлком равно х км. Какое уравнение соответствует условию задачи?
1) 3х = 2х + 25; 2) 3х = 2х — 25; 3) х/3 = х/2 + 25; 4) х/3 = х/2 — 25
2. Прочитайте задачу: От турбазы до автостанции турист доехал на велосипеде за 2 ч. Чтобы пройти это расстояние пешком, ему понадобилось бы 6 ч. Известно, что идёт он со скоростью, на 4 км/ч меньшей, чем едет на велосипеде. Найдите пешеходную скорость туриста.
Выберите уравнение, соответствующее условию задачи, если буквой х обозначена скорость (в км/ч), с которой турист идёт пешком.
1) 6х = 2(х — 4); 2) 6х = 2(х + 4); 3) 2х = 6(х — 4); 4) х/2 — х/6 = 4
3. Прочитайте задачу: Расстояние между двумя причалами по реке 14 км. На путь от одного причала до другого против течения моторная лодка затратила на 1 ч больше, чем на обратный путь по течению. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.
Пусть буквой х обозначена собственная скорость лодки (в км/ч). Какое уравнение соответствует условию задачи?
4. Все имеющиеся карандаши можно разложить в 3 большие коробки или в 5 маленьких. В маленькую коробку помещается на 6 карандашей меньше, чем в большую. Сколько всего имеется карандашей?
Пусть буквой х обозначено число карандашей в маленькой коробке. Выберите уравнение, соответствующее условию задачи.
1) х/3 — х/5 = 6; 2) 3х = 5(х — 6); 3) 5х = 3(х + 6); 4) 5х = 3(х — 6).
5. Фотографию прямоугольной формы, размеры которой 9х 13 см, наклеили на белую бумагу так, что вокруг всей фотографии получилась белая окантовка одной и той же ширины. Площадь, которую занимает фотография с окантовкой, равна 221 см2. Какова ширина окантовки?
Выберите уравнение, которое соответствует условию задачи.
1) 117 + 9х • 2 +13х • 2 = 221; 2) (9 + х)(13 + х) = 221
3) (13 + 2х) • 9 = 221; 4) (9 + 2х)(13 + 2х) = 221
6. Путь от посёлка до железнодорожной станции велосипедист проехал за 2 ч, а пешеход прошёл за 4,2 ч. Найдите длину пути от посёлка до станции, если известно, что скорость велосипедиста на 5 км/ч больше скорости пешехода.
Составьте уравнение по условию задачи, обозначив буквой х: 1) скорость велосипедиста; 2) длину пути от посёлка до станции.
7. Из прямоугольного листа картона, размеры которого 56 см и 32 см, надо сделать коробку без крышки. Для этого по углам листа вырезают одинаковые квадраты и загибают края вверх. Чему должна быть равна сторона вырезаемого квадрата, чтобы дно коробки имело площадь 640 см2?
Составьте уравнение по условию задачи, обозначив буквой х длину стороны вырезаемого квадрата (в см).
Решите задачу (№ 8—13):
8. От города до посёлка автомобиль доехал за 3 ч. Если бы водитель увеличил скорость на 25 км/ч, то затратил бы на этот путь 2 ч. Чему равно расстояние от города до посёлка?
9. Лодка проплыла от одной пристани до другой по течению реки за 3 ч, а обратный путь против течения у неё занял 4 ч. Найдите собственную скорость лодки, если скорость течения реки равна 2 км/ч.
10. Лодка плыла 5 ч против течения реки и затем 2 ч по течению. Всего она проплыла 40 км. Скорость течения реки равна 3 км/ч. Чему равна собственная скорость лодки?
11. Чему равны стороны прямоугольника, у которого одна из сторон на 6 см больше другой, а площадь равна 91 см2?
12. Ковёр прямоугольной формы со сторонами 4 м и 2,5 м покрывает ^ площади комнаты. Какова площадь комнаты?
13. В пакете 700 г смеси сухофруктов, состоящей из яблок, изюма и чернослива. Яблок в ней в 3 раза меньше, чем изюма, и на 100 г больше, чем чернослива. Сколько яблок в данной порции смеси?
ЗАДАНИЯ ПОВЫШЕННОГО УРОВНЯ
14. Из пунктов А и Ву расстояние между которыми 19 км, вышли одновременно навстречу друг другу два туриста и встретились в 9 км от пункта А. Найдите скорость каждого, если известно, что турист, вышедший из пункта Ау шёл со скоростью, на 1 км/ч большей, чем другой турист, и сделал в пути 30-минутную остановку.
15. Группа туристов отправляется на лодке от лагеря по течению реки с намерением вернуться обратно через 5 ч. Скорость течения реки 2 км/ч, скорость лодки в стоячей воде 8 км/ч. На какое наибольшее расстояние по реке они могут отплыть, если перед возвращением они планируют пробыть на берегу 3 ч?
16. Для сада выделили прямоугольный участок земли. Длина изгороди окажется меньше, если участок при той же площади будет иметь квадратную форму. Для этого надо одну сторону участка увеличить на 48 м, а другую уменьшить на 60 м. Какова длина стороны квадратного участка?
17. Из пункта А в пункт Д, расстояние между которыми 80 км, одновременно выехали два автобуса. Во время пути один из автобусов сделал остановку на 15 мин, но в пункт В прибыл на 5 мин раньше второго. Известно, что его скорость в 1,5 раза больше скорости другого. Найдите скорость каждого автобуса.
18. За определённое время на автозаводе должны были собрать 160 автомобилей. Первые 2 ч выполнялась установленная почасовая норма, а затем стали каждый час собирать на 3 автомобиля больше. В результате за 1 ч до срока было собрано 155 автомобилей. Сколько автомобилей в час планировали собирать первоначально?
19. Сколько граммов сахарного сиропа, концентрация которого 25 %, надо добавить к 200 г воды, чтобы в полученном растворе содержание сахара составило 5 %?
20. Влажность свежих грибов 90 %, а сухих — 15 %. Сколько сухих грибов получится из 1,7 кг свежих?