OSR-текст раздела (только текст)
Механические явления (коды ОГЭ 1.1 — 1.5) 1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Скорость. Ускорение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени. Материальной точкой считается тело, размеры которого малы по сравнению с другими характерными размерами, встречающимися при решении поставленной задачи. Траектория – воображаемая линия, вдоль которой движется тело. Относительность механического движения: 1. Механическое движение можно наблюдать только относительно других тел. Тело, относительно которого рассматривается механическое движение, называется телом отсчёта. 2. В различных системах отсчёта скорость и перемещение, характеризующие движение одного и того же тела, могут иметь разные модули и направления. 3. Координаты тела, траектория движения, путь зависят от выбора системы отсчёта, то есть для одного и того же тела могут быть разными. Основные физические величины, характеризующие механическое движение 1. Путь – длина траектории. Внимание! Путь не может быть отрицательным! 2. Перемещение – направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением. Проекция вектора перемещения на координатную ось sХ = x – x0 , где х0 – начальная координата тела, х – конечная координата тела. Модуль вектора перемещения может не совпадать по числовому значению с длиной пути. Его можно рассчитать с помощью проекций вектора перемещения на координатные оси 3. Средняя путевая скорость равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной! 4. Вектор средней скорости равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло: . В проекциях на координатную ось 0х . Внимание! Вектор средней скорости сонаправлен с вектором перемещения. 5. Мгновенная скорость – скорость тела в данной точке пространства в данный момент времени. Внимание! 1). Вектор мгновенной скорости направлен по касательной к траектории движения в каждой её точке. 2). Проекция перемещения на соответствующую координатную ось численно равна площади под графиком зависимости проекции скорости на эту ось от времени. 6. Ускорение – векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло: . В проекциях на координатную ось . Физический смысл: численно равно изменению скорости за 1 с. 1.2. Равномерное прямолинейное движение. Зависимость координаты тела от времени в случае равномерного прямолинейного движения. Графики зависимости от времени для проекции скорости, проекции перемещения, пути, координаты при равномерном прямолинейном движении Равномерное прямолинейное движение – прямолинейное движение, при котором скорость тела не меняется. Внимание! Для описания любого прямолинейного движения достаточно одной координатной оси. Уравнение движения – уравнение, выражающее зависимость координат от времени, например: x = x(t). Характер изменения основных величин, характеризующих движение 1. Ускорение. Равно нулю: а̅ = 0 . 2. Скорость. Не равна нулю, постоянна по величине и направлению: ʋ̅ = const. Для равномерного движения проекция вектора скорости равна отношению изменения координаты (проекции вектора перемещения) к тому промежутку времени, в течение которого это изменение произошло Физический смысл: численно равна изменению координаты (проекции вектора перемещения) за 1 с. 3. Перемещение. Вектор перемещения при равномерном прямолинейном движении прямо пропорционален времени: s = ʋt. В проекциях на координатную ось: sx = ʋxt. Внимание! Здесь и применительно к описанию зависимости других величин от времени под t понимается промежуток времени от начала движения (t0 = 0) ! В первом и во втором случае тело движется в направлении координатной оси Ох. Во втором случае тело движется в направлении, противоположном направлению оси Ох. По модулю ʋ1 > ʋ2 > ʋ3 (сравниваем модули перемещения за одинаковые промежутки времени). Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени: величина проекции вектора перемещения численно равна площади под графиком зависимости проекции скорости от времени. 4. Координата. Поскольку х = x0 + sx , зависимость координаты от времени описывается линейной функцией: х = x0 +vxt. На графике изображены следующие случаи движения. 1. Движение в направлении оси Ох, начальная координата отрицательна. 2. Движение в направлении оси Ох, начальная координата положительна. 3. Движение в направлении, противоположном направлению оси Ох, начальная координата равна нулю. 4. Движение в направлении оси Ох, начальная координата отрицательна. 5. Движение в направлении, противоположном направлению оси Ох, начальная координата положительна. 5. Путь. При равномерном прямолинейном движении в одном направлении равен модулю вектора перемещения: l = s. Внимание! Путь не может быть отрицательным! График зависимости проекции ускорения от времени График зависимости проекции вектора скорости на координатную ось от времени График зависимости проекции вектора перемещения на координатную ось от времени График зависимости координаты от времени 1.3. Прямолинейное равноускоренное движение. Зависимость координаты тела от времени в случае равноускоренного прямолинейного движения. Формулы для проекции перемещения, проекции скорости и проекции ускорения при равноускоренном прямолинейном движении. Графики зависимости от времени для проекции ускорения, проекции скорости, проекции перемещения, координаты при равноускоренном прямолинейном движении Прямолинейное равноускоренное движение – прямолинейное движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени. Основные величины, характеризующие движение. 1. Ускорение. Не меняется, то есть постоянно по величине и направлению: . Физический смысл: ускорение численно равно изменению скорости за 1 с. Например, ускорение равно 5 м/с2 – это значит, что скорость тела изменяется на 5 м/с за каждую секунду своего движения. 2. Мгновенная скорость. Меняется равномерно, увеличиваясь или уменьшаясь одинаково за равные промежутки времени. Уравнение, описывающее изменение скорости с течением времени: , в проекциях ʋx = ʋ0x + axt. На графике изображены следующие случаи движения. 1. Проекция начальной скорости больше нуля. то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью. 2. Проекция начальной скорости равна нулю. то есть тело движется в направлении координатной оси с увеличивающейся по модулю скоростью. 3. Проекция начальной скорости больше нуля, то есть тело движется в направлении координатной оси с уменьшающейся по модулю скоростью. 4. Проекция начальной скорости меньше нуля. то есть тело движется в направлении, противоположном направлению координатной оси, с уменьшающейся по модулю скоростью. 5. Проекция начальной скорости равна нулю. График зависимости проекции скорости на координатную ось от времени то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью. 6. Проекция начальной скорости отрицательна. то есть тело движется в направлении, противоположном направлению координатной оси, с увеличивающейся по модулю скоростью. 3. Перемещение. Зависимость перемещения от времени описывается квадратичной функцией: . В проекциях на координатную ось: . Иногда удобно пользоваться другими формулами для расчёта перемещения, которые получаются из исходной и уравнения зависимости проекции скорости от времени: Для расчёта проекции вектора перемещения удобно пользоваться графиком зависимости проекции скорости от времени. В случае, изображённом на рисунке: sx =S1 – S2, где S1, и S2 – числовые значения площадей треугольников. 4. Координата. Поскольку х = х0 + sx, зависимость координаты от времени тоже описывается квадратичной функцией: Если использовать другие варианты расчёта ускорения при равноускоренном движении, получаем: . 5. Путь. Если направление движения не меняется, то l = s. Если направление движения меняется, то l = s1 +s2, где s1 – модуль вектора перемещения до остановки, s2 – модуль вектора перемещения при движении в обратном направлении. Внимание! Путь не может быть отрицательным! 1.4. Свободное падение. Формулы, описывающие свободное падение тела по вертикали (движение тела вниз или вверх относительно поверхности Земли). Графики зависимости от времени для проекции ускорения, проекции скорости и координаты при свободном падении тела по вертикали Свободное падение – движение под действием одной силы тяжести, частный случай равноускоренного движения. Ускорение свободного падения обозначается особой буквой: . Оно одинаково для всех тел в данной точке планеты, направлено к центру планеты и равно g ~ 10 м/с2 (см. раздел 1.13). В зависимости от направления начальной скорости тела может реализовываться один из представленных ниже вариантов движения. Независимо от направления движения тела (вверх или вниз) для свободного падения справедливы формулы для расчёта основных кинематических величин при равноускоренном движении с учётом того, что ускорение заранее известно и равно g = const. Проекция вектора перемещения: Координата в любой момент времени: или 1.5. Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления центростремительного ускорения. Формула, связывающая период и частоту обращения Равномерное вращение – движение точки с постоянной по модулю скоростью (ʋ = const) по траектории, представляющей собой окружность. Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени проходит равные пути. Но так как скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит, равномерное движение по окружности – это ускоренное движение! Величины, характеризующие равномерное вращение 1. Линейная скорость равномерного вращения . По величине ʋ = l / t, где l – путь, пройденный по дуге окружности за промежуток времени t. Вектор линейной скорости в каждой точке направлен по касательной к дуге окружности в данной точке. 2. Период обращения . Время одного полного оборота: Т = t / N, где N – число полных оборотов за промежуток времени t. 3. Частота обращения . Число оборотов в единицу времени: v = N / t. Связана с периодом обращения соотношением v = 1 / T. Внимание! Полезно установить связь между линейной скоростью с другими параметрами обращения! За один полный оборот . 4. Центростремительное ускорение : где ʋ – модуль линейной скорости в данной точке окружности. Вектор центростремительного ускорения перпендикулярен вектору скорости и направлен по радиусу к центру окружности. Центростремительное ускорение меняет скорость по направлению, но не меняет по величине. При равномерном вращении центростремительное ускорение постоянно по величине и связано с периодом и частотой вращения соотношениями:
1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Скорость. Ускорение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости.
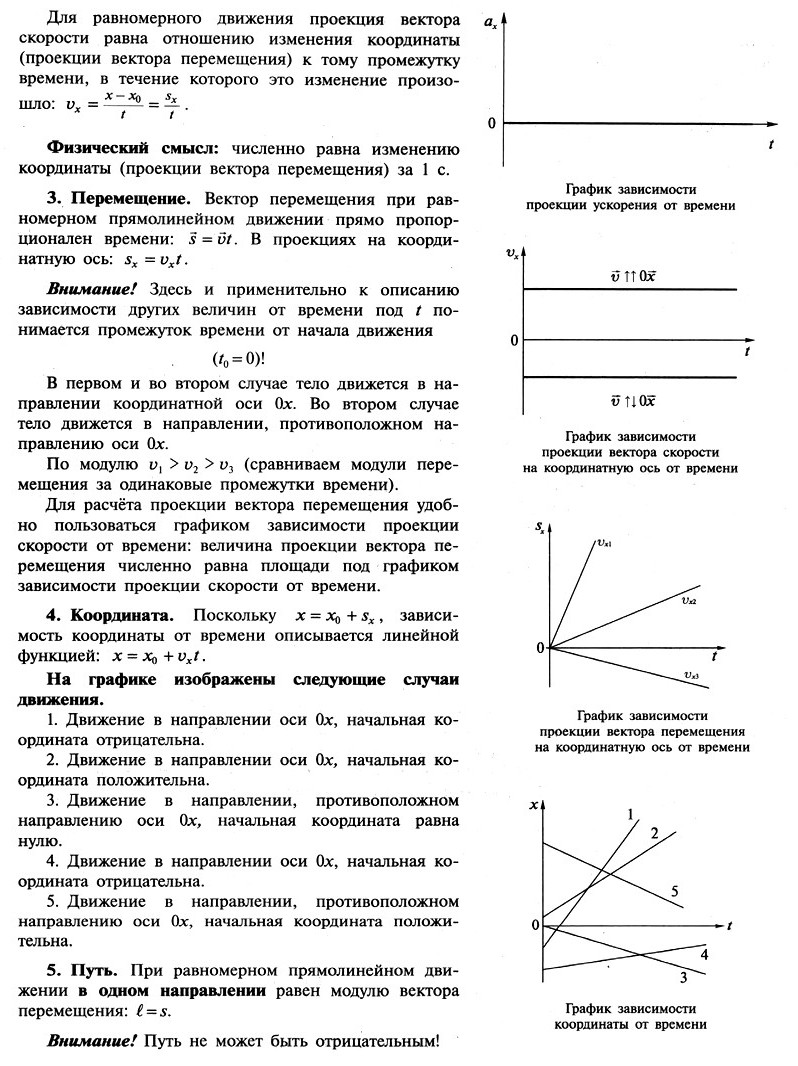
1.2. Равномерное прямолинейное движение. Зависимость координаты тела от времени в случае равномерного прямолинейного движения. Графики зависимости от времени для проекции скорости, проекции перемещения, пути, координаты при равномерном прямолинейном движении.
1.3. Прямолинейное равноускоренное движение. Зависимость координаты тела от времени в случае равноускоренного прямолинейного движения. Формулы для проекции перемещения, проекции скорости и проекции ускорения при равноускоренном прямолинейном движении. Графики зависимости от времени для проекции ускорения, проекции скорости, проекции перемещения, координаты при равноускоренном прямолинейном движении.
1.4. Свободное падение. Формулы, описывающие свободное падение тела по вертикали (движение тела вниз или вверх относительно поверхности Земли). Графики зависимости от времени для проекции ускорения, проекции скорости и координаты при свободном падении тела по вертикали.
1.5. Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления центростремительного ускорения. Формула, связывающая период и частоту обращения.