Механические явления (коды ОГЭ 1.16 — 1.23)

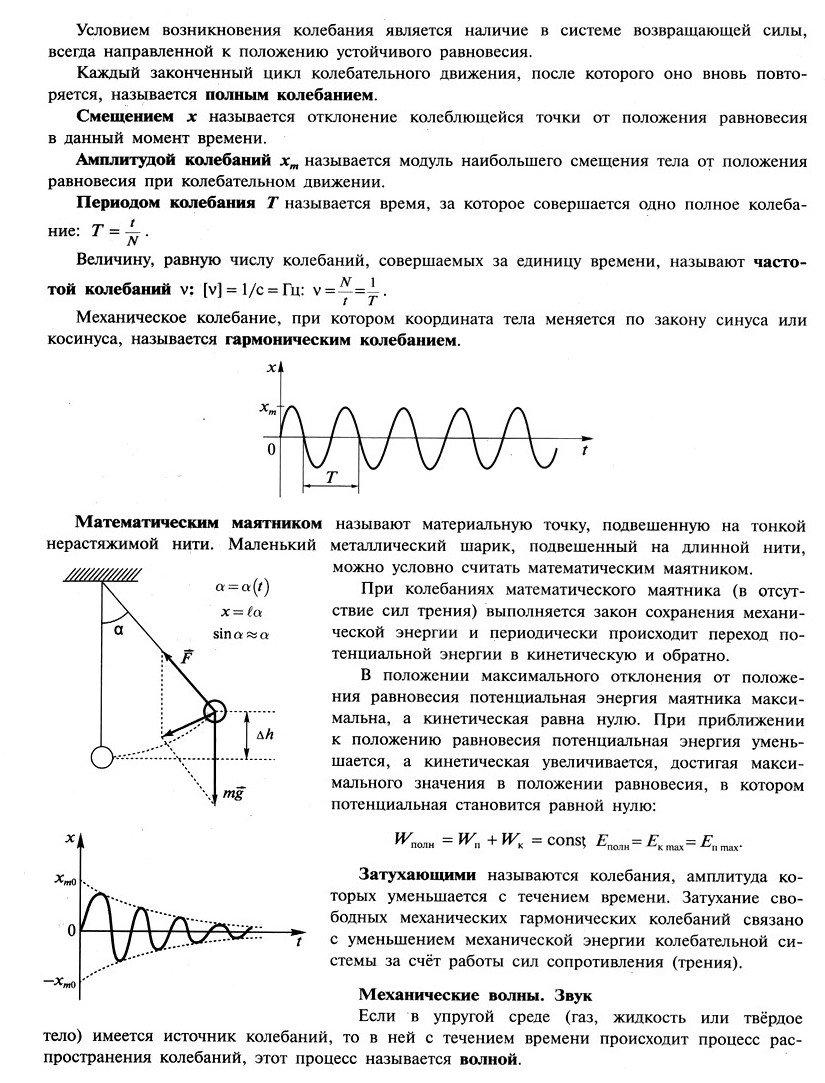
1.16. Механическая работа. Формула для вычисления работы силы. Механическая мощность Работа силы – физическая величина, характеризующая результат действия силы. Механическая работа А постоянной силы равна произведению модуля вектора силы на модуль вектора перемещения и на косинус угла а между вектором силы и вектором перемещения: А = Fs cos а. Единица измерения работы в СИ – джоуль: [А] = Дж = Н • м. Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы. Анализ формулы для расчёта работы показывает, что механическая работа не совершается если: – сила действует, а тело не перемещается; – тело перемещается, а сила равна нулю; – угол между векторами силы и перемещения равен 90° (cos a = 0). Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости. Работа – скалярная величина, она может быть как положительной, так и отрицательной. 1. Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна. 2. Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна. Работа обладает свойством аддитивности: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы. Примеры расчёта работы отдельных сил: Работа силы тяжести: не зависит от формы траектории и определяется только начальным и конечным положением тела: A = mg(h1 – h2). По замкнутой траектории работа силы тяжести равна нулю. Внимание! При движении вниз работа силы тяжести положительна, при движении вверх работа силы тяжести отрицательна. Работа силы трения скольжения: всегда отрицательна и зависит от формы траектории. Если сила трения не изменяется по модулю, то её работа А = –Fтр l где l – путь, пройденный телом (длина траектории). Очевидно, что чем больший путь проходит тело, тем большую по модулю работу совершает сила трения. Работа силы трения по замкнутой траектории не равна нулю! Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: Мощность показывает, какая работа совершается за 1 с. Единица измерения мощности в СИ – ватт: [ N ] = Дж/с = Вт. Мощность равна одному ватту, если за 1 с совершается работа 1 Дж. Может пригодиться! 1 л. с. (лошадиная сила) ~ 735 Вт. Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим . Для равноускоренного движения (F = const) где ʋср– средняя скорость движения за расчётный промежуток времени. 1.17. Кинетическая и потенциальная энергия. Формула для вычисления кинетической энергии. Формула для вычисления 7 потенциальной энергии тела, поднятого над Землёй Энергия – физическая величина, характеризующая состояние тела или системы тел. Причиной изменения состояния системы тел (изменения энергии) является работа внешних по отношению к рассматриваемой системе сил. В механике энергия тела или системы тел определяется взаимным положением тел (потенциальная энергия) и их скоростями (кинетическая энергия). Единица измерения энергии в СИ – джоуль. Кинетическая энергия – часть механической энергии, энергия движущегося тела. Скалярная величина, численно равная половине произведения массы тела на квадрат скорости: Теорема о кинетической энергии: Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии тела: A = Wk2 – Wk1 = ΔWk. Причём если А > 0, то Wk увеличивается, и если А < 0, то Wk уменьшается. Эта теорема справедлива для любого движения и для сил любой природы. Кинетическая энергия – величина относительная, зависящая от выбора СО, так как скорость тела зависит от выбора СО. Если тело разгоняется из состояния покоя, то Wk1 = 0, А = Wk2. Следовательно, физический смысл кинетической энергии: кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости. Внимание! Кинетическая энергия механической системы тел равна сумме кинетических энергий всех частей системы. Потенциальная энергия – часть механической энергии тела (системы тел), энергия взаимодействия тел или частей тела. Потенциальная энергия определяется взаимным расположением тел или частей тела, то есть расстояниями между ними. Потенциальная энергия относительна, зависит от выбора системы отсчёта, в частности от выбора тела отсчёта, которому соответствует нулевой уровень потенциальной энергии. Потенциальная энергия тела в поле силы тяжести численно равна произведению массы тела на ускорение свободного падения и на высоту относительно выбранного нулевого уровня: Wп = mgh. Связь работы силы тяжести и изменения потенциальной энергии: A = mg (h1 – h2) = – (mgh2 – mgh2) = – (Wп2 – Wп1) = – ΔWп Внимание! Работа сила тяжести равна изменению потенциальной энергии тела в поле силы тяжести, взятому с противоположным знаком. 1.18. Механическая энергия. Закон сохранения механической энергии. Формула для закона сохранения механической энергии в отсутствие сил трения. Превращение механической энергии при наличии силы трения Изменение механической энергии системы тел в общем случае равно сумме работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления: ΔW = Авнешн + Адиссип Если система тел замкнута (Авнешн = 0), то ΔW = Адиссип, то есть полная механическая энергия системы тел меняется только за счёт работы внутренних диссипативных сил системы (сил трения). Если система тел консервативна (то есть отсутствуют силы трения и сопротивления Атр = 0), то ΔW = Авнешн, то есть полная механическая энергия системы тел меняется только за счёт работы внешних по отношению к системе сил. Закон сохранения механической энергии: В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔW = 0 или Wп1 + Wк1 = Wп2 + Wк2 . Применим законы сохранения импульса и энергии к основным моделям столкновений тел. Абсолютно неупрутий удар (удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью). Импульс системы тел сохраняется, а полная механическая энергия не сохраняется: Абсолютно упругий удар (удар, при котором сохраняется механическая энергия системы). Сохраняются и импульс системы тел, и полная механическая энергия: Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом. 1.19. Простые механизмы. Золотое правило механики. Рычаг. Момент силы. Условие равновесия рычага. Подвижный и неподвижный блоки. КПД простых механизмов Простыми механизмами называются устройства, позволяющие совершить работу без применения источников немеханической энергии. С их помощью можно получить выигрыш в силе или изменить направление её действия. Золотое правило механики: При отсутствии трения выигрыш в силе равен проигрышу в расстоянии (простые механизмы не дают выигрыша в работе). Коэффициент полезного действия (КПД, ɳ) – физическая величина, равная отношению полезной работы (мощности, энергии) ко всей затраченной работе (мощности, энергии), выраженному в процентах: . Виды простых механизмов 1. Рычаг – твёрдое тело, имеющее закрёпленную ось вращения. Условие равновесия рычага: Суммарный момент сил, вращающих рычаг по часовой стрелке, равен суммарному моменту сил, вращающих рычаг против часовой стрелки. Момент силы М ([М] = Н • м) – физическая величина, равная произведению модуля силы на плечо: М = Fl. Плечо силы (l или d) относительно указанной точки – кратчайшее расстояние от точки до линии действия силы, то есть длина перпендикуляра, опущенного из точки на линию действия силы. Линия действия силы – прямая линия, на которой лежит вектор силы. Выигрыш в силе: Работа полезная: Ап = F1s1. Работа затраченная: Аз = F2s2. 2. Неподвижный блок (частный случай рычага). Выигрыш в силе: – выигрыша в силе нет, но меняется направление её действия. Работа полезная: Ап = F1s1. Работа затраченная: Аз = F2s2. 3. Подвижный блок (частный случай рычага). Выигрыш в силе: – выигрыш в силе в 2 раза. Работа полезная: Ап = F1s1. Работа затраченная: Аз = F2s2, при этом s2 =2s1. 4. Наклонная плоскость. Выигрыш в силе: = –. Работа полезная: Ап = mgh. Работа затраченная: Аз = Fl. 1.20. Давление твёрдого тела. Формула для вычисления давления твёрдого тела. Давление газа. Атмосферное давление. Гидростатическое давление внутри жидкости. Формула для вычисления давления внутри жидкости Силу, действующую перпендикулярно поверхности какого–либо тела, принято называть силой давления. Скалярная физическая величина, равная отношению модуля силы давления F к площади этой поверхности S, называется давлением: Единица измерения давления в СИ – паскаль (Па). Давление равно 1 Па, если на поверхность тела площадью 1 м2 действует сила давления 1 Н: Давление столба несжимаемой жидкости (гидростатическое давление): где h – высота столба жидкости, р – плотность жидкости. Внимание! На одном уровне гидростатическое давление одинаково во всех направлениях. Формула р = pgh определяет давление на любую площадку, помещённую на глубине h, независимо от того, как эта площадка расположена. Внимание! Давление столба жидкости (гидростатическое давление) зависит только от плотности жидкости и высоты столба жидкости и не зависит от формы сосуда, в том числе и от площади дна сосуда. Следовательно, оно не зависит от веса жидкости. В этом заключается гидростатический парадокс. Земля окружена воздушной оболочкой – атмосферой, состоящей из смеси различных газов. Слои воздуха, расположенные выше, давят на нижележащие слои, оказывая таким образом давление на поверхность Земли и на все находящиеся на ней тела. Это давление называется атмосферным. Атмосферное давление можно измерить с помощью столба жидкости. При переворачивании трубки, наполненной жидкостью, запаянным концом вверх часть жидкости выливается, а часть остаётся внутри трубки. На уровне свободной поверхности жидкости в широком сосуде (см. рисунок) давление столба жидкости высотой h уравновешивает атмосферное давление: ра = pgh. Первые опыты по измерению атмосферного давления проведены Э. Торричелли. В качестве жидкости использовалась ртуть. Внимание! Атмосферное давление, уравновешиваемое при 0°С столбом ртути высотой 760 мм, считается нормальным и называется физической атмосферой (атм). Давление, производимое столбом ртути высотой 1 мм, называется миллиметром ртутного столба (мм рт. ст.): – 1 атм = 760 мм рт. ст. = 101325 Па ~ 105 Па; – 1 мм рт. ст. ~ 133,3 Па. Приборы для измерения атмосферного давления называются барометрами. Приборы, измеряющие разницу между давлением газа в сосуде и атмосферным давлением, называются манометрами. 1.21. Закон Паскаля. Гидравлический пресс Для жидкостей и газов справедлив закон Паскаля: Жидкости и газы передают оказываемое на них давление без изменения по всем направлениям во все точки жидкости или газа. Закон Паскаля позволяет объяснить особое свойство сообщающихся сосудов, то есть сосудов, соединённых между собой каналом, заполненным жидкостью. Закон сообщающихся сосудов: В сообщающихся сосудах однородная жидкость всегда устанавливается на одном уровне. Жидкость находится в покое, поэтому на любом уровне (см. пунктир на рисунке) давление в левом сосуде должно равняться давлению в правом сосуде: pа + p1gh1 = pа + p2gh2 => h1 = h2 Внимание! Если в сообщающихся сосудах находятся две несмешивающиеся жидкости разными плотностями, то уровни жидкостей будут разными. Из равенства pа + p1gh1 = pа + p2gh2 следует, что отношение высот столбов жидкостей по отношению любому уровню, выше которого в каждом из сосудов находятся жидкости одного сорта, равно обратному отношению плотностей: Гидравлический пресс представляет собой два сообщающихся сосуда с различной площадью поперечного сечения, в которых имеются поршни, плотно прилегающие к стенкам сосудов. Давление, оказываемое на поршень меньшей площади, в соответствии с законом Паскаля передаётся без изменения во все точки жидкости, в том числе находящиеся непосредственно под вторым поршнем: Гидравлический пресс даёт выигрыш в силе, равный отношению площади большего поршня к площади меньшего поршня: Внимание! Как и в других простых механизмах, выигрыша в работе нет: при опускании малого поршня совершается работа, равная работе, совершаемой при подъёме большего поршня (если отсутствуют силы трения и сопротивления). 1.22. Закон Архимеда. Формула для определения выталкивающей силы, действующей на тело, погружённое в жидкость или газ. Условие плавания тел. Плавание судов и воздухоплавание Выталкивающая сила, действующая на тело со стороны жидкости и газа (общий случай) Увеличение гидростатического давления по мере погружения в жидкость или газ является причиной возникновения выталкивающей силы: Fвыт = F1 – F2. Сила Архимеда – выталкивающая сила, действующая на тело со стороны жидкости (газа) в случаях, если: – тело полностью погружено в жидкость (газ), при этом со всех сторон окружено жидкостью (газом); – тело плавает на поверхности жидкости, частично погрузившись в неё. FA = pжgVпчт, где рж – плотность жидкости (газа), Vпчт – объём погружённой в жидкость части тела. Так как ржVпчт = mж– масса жидкости (газа), вытесненной телом, то Vвыт = FА = mвыт.жg = Pвыт.ж Закон Архимеда: На тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (газа), вытесненной телом. . Внимание! Выталкивающую силу не всегда удаётся рассчитать с помощью формулы FА = ржgVпчт. Например, часть поверхности тела площадью S плотно соприкасается с дном сосуда. В этом случае выталкивающая сила будет равна F = pжgVт – FдS, где Fд – сила гидростатического давления жидкости на уровне дна сосуда. 1. Если тело плотно прилегает ко дну, значит, под телом жидкости нет и нет силы давления, направленной вверх. Архимедова сила не действует, тело прижимается верхним слоем жидкости ко дну. 2. Если какая-то часть поверхности тела плотно прилегает ко дну, а под другой частью поверхности есть жидкость, то нужно провести расчёт выталкивающей силы для данного конкретного случая. Для этого нужно подсчитать силы давления, действующие на верхнюю поверхность тела, и те части нижней поверхности тела, под которыми находится слой жидкости. Условия плавания тел 1. Тело целиком погружено в жидкость. Выталкивающая сила больше силы тяжести: Fвыт > mg (ржидкости > ртела). Тело всплывает до тех пор, пока силы не уравновесятся за счёт уменьшения выталкивающей силы (уменьшается объём погружённой в жидкость части тела). 2. Тело целиком погружено в жидкость. Выталкивающая сила равна силе тяжести: Fвыт = mg (ржидкости = ртела). Тело плавает в любой точке жидкости (газа). 3. Тело целиком погружено в жидкость. Выталкивающая сила меньше силы тяжести: Fвыт < mg (ржидкости < ртела). Тело тонет. 1.23. Механические колебания и волны. Амплитуда, период и частота колебаний. Формула, связывающая частоту и период колебаний. Механические волны. Продольные и поперечные волны. Длина волны и скорость распространения волны. Звук. Громкость и высота звука. Скорость распространения звука. Отражение и преломление звуковой волны на границе двух сред. Инфразвук и ультразвук Движение, при котором состояния движущегося тела с течением времени повторяются, причём тело проходит через положение своего устойчивого равновесия поочерёдно в противоположных направлениях, называется механическим колебанием. Условием возникновения колебания является наличие в системе возвращающей силы, всегда направленной к положению устойчивого равновесия. Каждый законченный цикл колебательного движения, после которого оно вновь повторяется, называется полным колебанием. Смещением х называется отклонение колеблющейся точки от положения равновесия в данный момент времени. Амплитудой колебаний хm называется модуль наибольшего смещения тела от положения равновесия при колебательном движении. Периодом колебания Т называется время, за которое совершается одно полное колебание: Т = t/N. Величину, равную числу колебаний, совершаемых за единицу времени, называют частотой колебаний Механическое колебание, при котором координата тела меняется по закону синуса или косинуса, называется гармоническим колебанием. Математическим маятником называют материальную точку, подвешенную на тонкой нерастяжимой нити. Маленький металлический шарик, подвешенный на длинной нити, можно условно считать математическим маятником. При колебаниях математического маятника (в отсутствие сил трения) выполняется закон сохранения механической энергии и периодически происходит переход потенциальной энергии в кинетическую и обратно. В положении максимального отклонения от положения равновесия потенциальная энергия маятника максимальна, а кинетическая равна нулю. При приближении к положению равновесия потенциальная энергия уменьшается, а кинетическая увеличивается, достигая максимального значения в положении равновесия, в котором потенциальная становится равной нулю: Wполн = Wп + Wк = const Eполн = Eк max = Еп maх. Затухающими называются колебания, амплитуда которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с уменьшением механической энергии колебательной системы за счёт работы сил сопротивления (трения). Механические волны. Звук Если в упругой среде (газ, жидкость или твёрдое тело) имеется источник колебаний, то в ней с течением времени происходит процесс распространения колебаний, этот процесс называется волной. Волны, распространяющиеся в упругой среде, называются механическими волнами. В волне осуществляется перенос энергии колебательного движения без переноса вещества (массы) среды, в которой распространяется волна. Периодом Т волны является период колебаний точек среды при распространении волны. Длиной волны λ называется расстояние, на которое распространяется волна за один период колебаний: λ = ʋT; ʋ = λv. Продольными волнами называются волны, в которых направление колебаний частиц происходит в направлении распространения волны. Продольные механические волны могут распространяться в твёрдых, в жидких и в газообразных средах. Поперечными называются волны, в которых направление колебаний частиц происходит перпендикулярно направлению распространения волны. Поперечные механические волны могут распространяться только в твёрдых телах и на свободной поверхности жидкости. Звуковыми волнами называются механические волны, вызывающие у человека ощущение звука: ʋзв = (16 ÷ 20 000) Гц. Характеристики звука Громкость звука определяется амплитудой колебаний. Высота тона определяется частотой колебаний. Скорость звука зависит от плотности среды. Скорость звука в твёрдых телах больше, чем в жидкостях, а в жидкостях больше, чем в газах. Скорость звука увеличивается с ростом температуры среды. В случае, когда отражающая поверхность перпендикулярна распространению волны, звуковая волна после отражения возвращается обратно к источнику звука. Такой случай отражения называется эхом. В гидролокации эхо используется для определения глубин, расстояний до преград и других судов.