Справочник ОГЭ по математике. Раздел 3.3. Текстовые задачи.
Содержание:
3.3.1. Решение текстовых задач арифметическим способом
3.3.2. Решение текстовых задач алгебраическим способом.
ОГЛАВЛЕНИЕ Перейти в другие разделы:
3.2 …
4.1
3.3. Текстовые задачи.
Вы смотрели конспект по математике «3.3. Текстовые задачи (справочник ОГЭ)».
Выберите дальнейшее действие:
OCR-версия текста страницы:
3.3.1. Решение текстовых задач арифметическим способом
Задачи на масштаб Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты. Например, масштаб карты 1 : 100 000 означает, что 100 000 см на местности соответствует 1 см на карте. Масштаб географической карты — это частное, меньшее единицы. Существуют масштабы больше единицы, например, технические чертежи, изображения, полученные с помощью микроскопа, и т. д. Например, масштаб 9:1 означает, что размер предмета на чертеже увеличен в 9 раз.
Задача 1. Трубопровод длиной 50 км изображен на карте отрезком 2,5 см. Найти масштаб карты. Решение: Переведем длину трубопровода в сантиметры: 50 км = 50 000 м = 5 000 000 см. Найдем отношение длины отрезка на карте и длины отрезка на местности: 2,5 : 5 000 000 = 25 : 50 000 000 = 1 : 2 000 000. Ответ: 1 : 200 000.
Задача 2. Длина железнодорожной магистрали из Москвы до Курска приближенно равна 540 км. Какой длины будет линия, изображающая эту магистраль, на карте, сделанной в масштабе 1 : 10 000 000? Решение: 1) 540 км = 540 000 м = 54 000 000 (см); 2) 54 000 000 : 10 000 000 = 5,4 (см). Ответ: 5,4 см. Задача 3. На плане изображен участок земли в виде прямоугольника со сторонами 2 и 8 см. Чему равна площадь этого участка, если масштаб плана 1 : 1500? Решение: Найдем стороны прямоугольного участка на местности: 2 см • 1500 = 3 000 см = 30 м; 8 см • 1500 = 12 000 см = 120 (м). Тогда площадь участка: 30 • 1200 = 36 000 м2 = 3,6 (га). Ответ: 3,6 га.
Задача 4. Деталь на чертеже, выполненном в масштабе 5 : 1, имеет длину 2,7 см. Какую длину будет иметь деталь на чертеже, выполненном в масштабе 9 : 1? Решение: Масштаб 5 : 1 означает, что истинные размеры детали в пять раз больше, чем на чертеже, т. е. 2,7 см • 5. Масштаб 9 : 1 означает, что изображение детали на чертеже уменьшат в 9 раз, т. е. длина детали на этом чертеже будет: Ответ: 1,5 см.
Задачи на нахождение среднего арифметического нескольких чисел Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых:
Задача 1. Во время соревнований по фигурному катанию за произвольную программу спортсменка получила следующие оценки: 5,9; 5,8; 5,9; 5,7 и 6,0. Каков средний балл, полученный фигуристкой в этом виде катания? Решение: Найдем среднее арифметическое этих пяти чисел: Ответ: 5,86.
Задача 2. Поезд шел 4 ч со скоростью 72 км/ч и 2 ч со скоростью 84 км/ч. Найти среднюю скорость поезда на этом участке пути. Решение: Весь путь составит: 72 • 4 + 84 • 2 = 456 (км), время движения: 4 + 2 = 6 (ч), тогда средняя скорость равна: 456 : 6 = 76 (км/ч). Ответ: 76 км/ч. Среднюю скорость можно найти так: Аналогично можно найти среднюю урожайность, среднюю производительность и т. д. Если известно среднее арифметическое, то сумму чисел можно найти так: Сумма чисел = (среднее арифметическое) • (количество чисел).
Задача 3. Средний возраст 11 футболистов — 23 года. Во время игры одного футболиста удалили, и средний возраст футболистов стал 22 года. Сколько лет удаленному футболисту? Решение: Средний возраст 11 футболистов — 23 года, значит общая сумма их возрастов: 23 • 11 = 253 (года). После удаления одного игрока футболистов осталось 10, их средний возраст: 22 • 10 = 220 (лет). Значит, удалили футболиста, которому: 253 – 220 = 33 (года). Ответ: 33 года.
Задачи на движение Пусть во всех задачах автомобиль движется со скоростью 80 км/ч, а мотоциклист — со скоростью 50 км/ч.
Задача 1. Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоциклист. Какое расстояние будет между ними через 1 ч, 2 ч, через какое время они встретятся? Расстояние между городами 325 км. Решение: Количество километров, на которое за единицу времени сближаются автомобиль и мотоцикл, называют скоростью сближения. В данном случае: 80 + 50 = = 130 (км/ч). За один час они сблизятся на 130 км. 50 км/ч 80 км/ч За два часа они сблизятся на: 130 • 2 = 260 (км). Встретятся через: 325 : 130 = 2,5 (ч). РиС. 3.49 Ответ: 130 км; 260 км; 2,5 ч. Задача 2. После встречи автомобиль и мотоцикл отправились в противоположные стороны. На какое расстояние они удалятся друг от друга за 1 ч, за 2 ч? Решение: Количество километров, на которое за единицу времени удаляются автомобиль и мотоцикл, называется скоростью удаления друг от друга. Это: 80 + 50 = = 130 (км). За час они удалятся на 130 км. За два часа — на: 130 • 2 = 260 (км). Ответ: 130 км; 260 км. При движении навстречу друг другу (в стороны друг от друга) скорость сближения (удаления) равна сумме скоростей.
Задача 3. Автомобиль и мотоцикл выехали одновременно в одну сторону из двух пунктов, расстояние между которыми 390 км. На какое расстояние они сблизятся через 1 ч, 2 ч, когда автомобиль догонит мотоцикл? Решение: Расстояние между автомобилем и мотоциклом будет сокращаться каждый час на: 80 – 50 = 30 (км). 80 км/ч 50 км/4 За 1 ч они сблизятся на 30 км, за 2 ч — на: 30 • 2 = 60 (км). Автомобиль догонит мотоцикл че– Рис 350 рез: 390 : 30 = 13 (ч). Ответ: 30 км; 60 км; 13 ч.
Задача 4. Автомобиль и мотоцикл одновременно выехали из одного пункта в одном направлении. При этом автомобиль удаляется от мотоцикла. На какое расстояние они удалятся друг от друга за 1 ч, 2 ч? Решение: Расстояние между автомобилем и мотоциклом каждый час будет увеличиваться на: 80 – 50 = = 30 (км). За 1 ч они удалятся на 30 км, за 2 ч — на: 0 • 2 = = 60 (км). Ответ: 30 км; 60 км. При движении в одном направлении скорость сближения (удаления) равна разности скоростей.
Задача 5. Расстояние между селом и городом 280 км. Из села в город выехал легковой автомобиль. Одновременно с ним из города в село выехала грузовая машина. Сколько километров проехала грузовая машина до встречи с легковым автомобилем, если грузовая машина двигалась со скоростью 48 км/ч, что составляло 3/4 от скорости легкового автомобиля? Решение: Ответ: 120 км. Движение по течению и против течения Скорость движения по течению = скорость собственная + скорость течения. Скорость движения против течения = скорость собственная — скорость течения.
Задача 6. Катер движется по течению реки со скоростью 15,2 км/ч, а против течения — 8,2 км/ч. Какова скорость течения? Решение: Скорость движения по течению отличается от скорости движения против течения на две скорости течения, т. е. скорость течения: (15,2 – 8,2) : 2 = 3,5 (км/ч). Ответ: 3,5 км/ч.
Задача 7. Моторная лодка прошла 207 км по течению реки за 13,5 ч, потратив часть времени на остановки. Скорость течения реки 1,75 км/ч. Сколько километров может пройти эта лодка за 2 ч против течения? Решение: 1) 13,5 – 13,5 • = 13,5 – 1,5 = 12 (час) — время движения лодки по течению без остановок; 2) 207 : 12 = 17,25 (км/ч) — скорость по течению; 3) 17,25 – 1,75 = 15,5 (км/ч) — собственная скорость лодки; 4) 15,5 – 1,75 = 13,75 (км/ч) — скорость против течения; 5) 13,75 • 2 = 27,5 (км) — пройдет лодка за 2 ч против течения. Ответ: 27,5 км. Задачи на совместную работу Если в задачах на совместную работу не указан объем работ, то всю работу принимают за единицу. Кроме того, в этих задачах рассматривается время, в течение которого производится работа, и производительность, т. е. работа, произведенная в единицу времени.
Задача 8. Два тракториста вспахали поле за 12 ч. Один тракторист, работая самостоятельно, может вспахать поле за 30 ч. За сколько вспахал бы поле второй тракторист, работая сам? Решение: Если два тракториста вспахали поле за 12 ч, значит, за 1 ч они вспашут часть поля. Первый тракторист вспашет все поле за 30 ч, а за 1 ч Тогда второй тракторист вспашет: часть поля. Значит, 60 20 второй тракторист, работая сам, вспашет поле за 20 ч. Ответ: 20 ч.
Задача 9. В бассейн проведено три трубы: через первую трубу бассейн может наполниться за 6 ч, через другую — за 4 ч, а через третью трубу вся вода из наполненного бассейна может вытечь за 12 ч. За какое время может наполниться половина бассейна, если открыть все три трубы? Решение: За 1 ч первая труба наполняет 1 часть, вторая — 1 часть, через третью вытекает часть. То есть за 1 ч наполнится: часть бассейна. Тогда весь бассейн наполнится за 3 ч, а половина бассейна — за 1,5 ч. Ответ: 1,5 ч.
Задачи на дроби и отношения Задача 10. За первый день турист прошел часть пути, за второй — оставшегося пути, а за третий — остальные 30 км. Какое расстояние прошел турист за три дня? Решение: часть пути прошел турист за второй и третий день вместе; прошел турист за второй день; 4 Ответ: 72 км.
Задача 11. В первой школе 840 учеников, во второй — на 7 этого числа больше, 53 в третьей — 3 числа учеников второй школы, а в четвертой — 33 числа учеников первых трех школ вместе. Сколько учеников в четырех школах вместе? Ответ: 3 380 учеников.
Задача 12. В двух слитках серебра массой 300 г и 400 г различное процентное содержание серебра. Каждый из слитков следует разделить на две части так, чтобы из получившихся четырех кусков можно было изготовить два слитка массой 200 г и 500 г с равным процентным содержанием серебра. На какие части следует разделить каждый слиток? Решение: Очевидно, что в новых слитках, т. е. слитках массой 200 г и 500 г, процентное содержание серебра должно быть таким же, как и в слитке массой 700 г, получившемся бы при сплавлении вместе исходных слитков. Следовательно, отношение, в котором в каждый новый слиток входят части исходных, должно быть: 300 : 400 = 3 : 4. Получили задачу: разделить заданную величину на части, пропорциональные числам 3 : 4. 200–граммовый слиток должен содержать: — исходного первого слитка; (г) — исходного второго. Аналогично для 400–граммового слитка: Ответ: слиток массой 300 г следует разделить на части
3.3.2. Решение текстовых задач алгебраическим способом Задачи на движение При решении задач на движение используется формула: s = v ■ t где v — скорость движения, t — время, s — расстояние, пройденное за время t со скоростью v. Отсюда получим формулы: .
Задача 1. Пассажир, ехавший в поезде со скоростью 60 км/ч, заметил, что встречный поезд прошел мимо него за 2,5 с. Определить скорость встречного поезда, если его длина 100 м. Решение: Пусть скорость встречного поезда х км/ч, тогда его скорость относительно пассажира — (х + 60) км/ч. 100 м = 0,1 км. Воспользуемся формулой t – , получим уравнение Ответ: 84 км/ч.
Задача 2. Дорогу от A до B велосипедист проезжает со скоростью v1 км/ч, а обратную дорогу от B до A — со скоростью v2 км/ч. Определить среднюю скорость велосипедиста. Решение: Пусть s — расстояние от A до B, t1 и t2 — время, затраченное велосипедистом соответственно на прямой и обратный путь, тогда t1 = — и t2 = —. Общее время пути: t – t1 + t . За это время велосипедист преодолевает расстояние 2s. Тогда средняя скорость: Получим уравнение: v • 30 км/ч, то: v = = 24 км/ч. Например, если v1 = 20 км/ч и v2 Ответ:
Задача 3. Дорога от A до B длиной 11,5 км идет сначала вверх, потом по ровному участку и затем вниз. Пешеход, идя из A в B, прошел дорогу за 2 ч 54 мин, а на обратную дорогу затратил 3 ч 6 мин. Скорость пешехода: вверх — 3 км/ч, по ровному участку — 4 км/ч, вниз — 5 км/ч. Найти протяженность ровного участка пути. Решение: Пусть при движении от A до B х — длина дороги вверх, у — длина ровного участка, тогда (11,5 – х –– у) — длина дороги вниз. При движении от B до A имеем: (11,5 – х – у) — протяженность пути вверх, х — протяженность пути вниз. При движении от A до B: — время движения вверх; — время движения по ровному участку; — время движения вниз. Аналогично при движении от B до A: — время движения вверх; — время движения вниз; — время движения по ровному участку. 54 Получим систему уравнений: Ответ: 4 км. Составление неравенств в задачах на движение
Задача 4. Велосипедист выехал из A в B. Расстояние от A до B равно 60 км, скорость велосипедиста постоянна. Не задерживаясь в B, он едет обратно с той же скоростью, но через час после выезда из B делает остановку на 20 мин. После этого он продолжает путь, увеличив скорость на 4 км/ч. В каком интервале заключена скорость v велосипедиста, если известно, что на обратный путь от B до A он потратил времени не более, чем от A до B? Решение: Пусть первоначальная скорость велосипедиста — х км/ч. Тогда время его движения из A и B равна tAB = ч, а обратно — tBA = + 1ч. По условию tBA tAB, тогда: Решим неравенство методом интервалов: Поскольку скорость не может быть отрицательной, то нам подходит только промежуток (0; 20]. Ответ: 0 v 20 км/ч. Задачи на движение тел по окружности
Задача 5. По окружности длиной 60 м равномерно и в одном направлении движутся две точки. Одна из них делает полный оборот на 5 с быстрее другой. При этом точки встречаются каждый раз через 1 мин. Определить скорости точки. Решение: Пусть х с — время, за которое первая точка делает полный оборот, вторая точка — за у с. Тогда скорости точек соответственно: Пусть х у, тогда по условию у – х – 5. Поскольку точки встречаются каждую минуту и первая движется быстрее, она должна за 1 мин пройти полный круг 60 м и еще столько, сколько успеет пройти за 1 мин вторая точка, т. е. Получим второе уравнение: через 1 мин Составим систему: Решим систему способом подстановки: у – х + 5. 60(х + 5) – 60х = х(х + 5); х2 – 5х – 300 = 0; х1 = 15; х2 = –20 — не удовлетворяет условию задачи. х – 15, у – 20. Тогда v1 = — = 4 (м/с); v2 = 55 = 3 (м/с). Ответ: 4 м/с; 3 м/с.
Задача 6. Пассажирский и товарный поезда выехали одновременно навстречу друг другу из двух городов, расстояние между которыми 1080 км. Пассажирский поезд проходил за 1 ч на 10 км больше, чем товарный. Найти скорость каждого поезда, если через 5 ч после выхода расстояние между ними составило 630 км. Решение: Пусть х км/ч — скорость товарного поезда. Поместим данные в таблицу. 5x км 630 км 5(x + 10) км 1080 км Рис. 3.56 Общий путь составит: 5х + 5(х + 10) + 630 = 1080; 5х + 5х + 50 + 630 = 1080; х – 40; х + 10 = 50. Ответ: 40 км/ч, 50 км/ч.
Задача 7. С аэродрома вылетают одновременно в пункт, который удален от него на 2 400 км, два самолета. Скорость одного из них на 120 км/ч больше скорости Вид транспорта v, км/ч t, ч s, км Товарный поезд х 5 5х Пассажирский поезд х + 10 5 5(х + 10) другого, поэтому он прилетит в пункт назначения на час раньше. Найти скорость каждого самолета. Решение: Пусть скорость одного самолета — х км/ч, тогда второго — (х + 120) км/ч. Поместим данные в таблицу. Самолет v, км/ч t, ч s, км Первый (с меньшей скоростью) х 2 400 2 400 Второй (с большей скоростью) х + 120 2 400 2 400 Поскольку величина на 1 час больше, чем , получим уравнение: 2 400(х + 120) – 2 400х = х(х + 120); х2 + 120х – 288 000 = 0; х1 = –600, х2 = 480. х1 — не удовлетворяет условию задачи, х – 480, х + 120 = 600. Ответ: 480 км/ч и 600 км/ч.
Задачи на движение по реке (по течению и против течения) Если собственная скорость лодки (катера и т. д.), v — скорость течения реки, то скорость по течению: , скорость против течения: Задача 8. Катер проплыл 9 км по течению реки и 14 км против течения, затратив на весь путь столько времени, сколько ему потребуется, чтобы проплыть 24 км в стоячей воде. Найти собственную скорость катера, если скорость течения реки 2 км/ч. Решение: Пусть скорость катера в стоячей воде (т. е. собственная скорость катера) — х км/ч. Поместим данные в таблицу. Направление движения v, км/ч t, ч s, км В стоячей воде х 24 24 Время движения по течению и против течения равно времени движения в стоячей воде. Получим уравнение: Число –6 не удовлетворяет условию задачи, х — 16. Ответ: 16 км/ч.
Задача 9. Моторной лодке, чтобы пройти 12 км по течению реки и возвратиться назад, необходимо 2,5 ч. За 1 ч 20 мин она проходит 4 км по течению реки и 8 км против течения. Найти скорость лодки в стоячей воде (собственную скорость) и скорость течения реки. Решение: Пусть х — собственная скорость лодки, у — скорость течения реки. Поместим данные в таблицы. Общее время движения — 2,5 ч Общее время движения — Направление движения v, км/ч t, ч s, км По течению х + у 12 12 Против течения X – у 12 12 Направление движения v, км/ч t, ч s, км По течению х + у 4 4 Против течения х – у 8 8 Получим систему уравнений: Сделаем замену: t1 — t2 — , получим систему: Возвращаемся к переменным x и у: Ответ: 10 км/ч и 2 км/ч. Задачи на совместную работу В задачах на работу содержатся следующие величины: t — время, в течение которого производится работа; N — производительность, т. е. работа, произведенная в единицу времени; A — работа, произведенная за время t. Эти три величины связывает уравнение: A = Nt Если в задаче не указано, какой конкретно объем работы выполняется, то работу принимают за единицу. В задачах на перекачивание жидкости насосами за единицу принимают объем перекачанной жидкости.
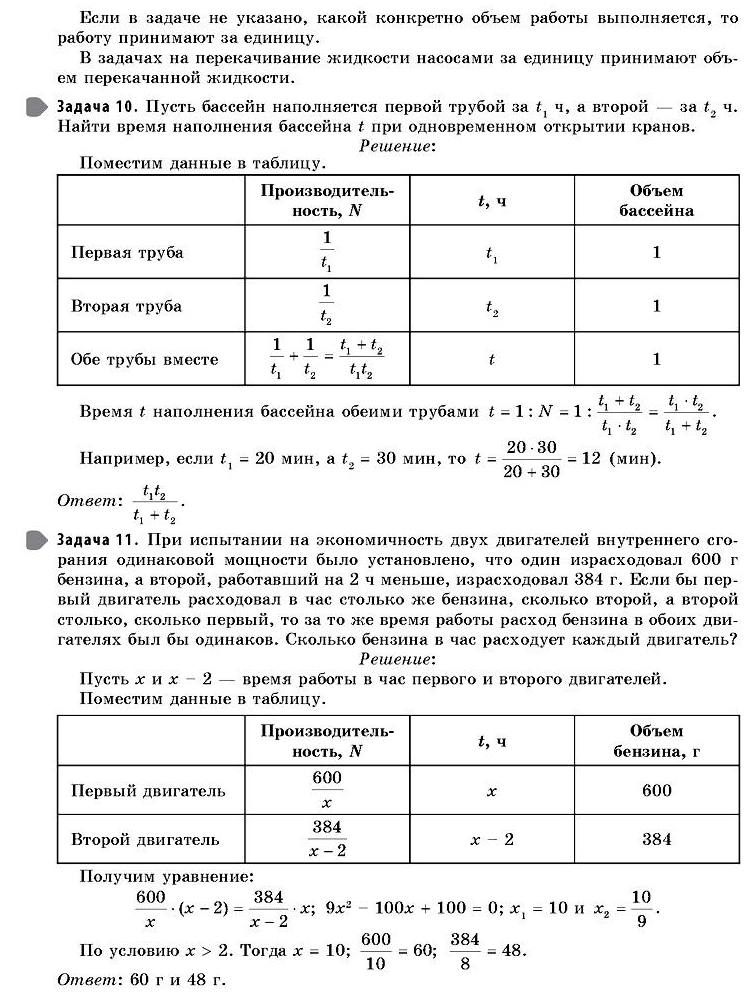
Задача 10. Пусть бассейн наполняется первой трубой за t1 ч, а второй — за t2 ч. Найти время наполнения бассейна t при одновременном открытии кранов. Решение: Поместим данные в таблицу. Время t наполнения бассейна обеими трубами Например, если t1 = 20 мин, а t2 = 30 мин, то t — Ответ:
Задача 11. При испытании на экономичность двух двигателей внутреннего сгорания одинаковой мощности было установлено, что один израсходовал 600 г бензина, а второй, работавший на 2 ч меньше, израсходовал 384 г. Если бы первый двигатель расходовал в час столько же бензина, сколько второй, а второй столько, сколько первый, то за то же время работы расход бензина в обоих двигателях был бы одинаков. Сколько бензина в час расходует каждый двигатель? Решение: Пусть х и х – 2 — время работы в час первого и второго двигателей. Поместим данные в таблицу. Получим уравнение: По условию х > 2. Тогда х – 10; Ответ: 60 г и 48 г.
Задача 12. Двое рабочих заняты на одной и той же работе. Сначала один проработал треть того времени, которое требуется второму для выполнения всей работы, потом второй проработал треть того времени, которое потратил бы первый на выполнение всей работы. После этого оказалось, что выполнено всей работы. Определить, сколько времени потребовалось бы для выполнения работы каждому рабочему, если вместе они могут выполнить ее за 1 ч 20 мин. Решением является пара чисел (2; 4) или (4; 2). Ответ: 2 ч; 4 ч.
Задачи на планирование Задачи на планирование — это задачи на совместную работу, в которых выполняемый объем работы известен или его нужно определить. При этом сравнивается работа, которая должна быть выполнена по плану, и работа, которая выполняется фактически. Как и в задачах на совместную работу, основными компонентами являются: а) работа (выполненная фактически и запланированная); б) время выполнения работы (фактическое и запланированное); в) производительность труда (фактическая и запланированная).
Задача 13. Ученик токаря вытачивает шахматные пешки для определенного количества шахматных комплектов. Если он будет изготовлять на 2 пешки больше, то выполнит задание на 10 дней быстрее. Если он сможет изготовлять ежедневно на 4 пешки больше, то срок исполнения задания уменьшится на 16 дней. Сколько шахматных комплектов обеспечивает пешками этот токарь, если для каждого комплекта нужно 16 пешек? Решение: Пусть x — количество пешек для определенного числа комплектов шахмат, а в день он вытачивает у пешек. Поместим данные в таблицу. По условию задачи получаем систему уравнений: Ответ: 15 комплектов.
Задачи на смеси и сплавы Задача 14. Смешали 30 % –й и 10 %–й растворы соляной кислоты и получили 600 г 15 %–го раствора. Сколько граммов каждого раствора было взято? Решение: Ответ: 150 г 30 %–го раствора и 450 г 10 %–го раствора. Задача 15. Определить пробу сплава серебра с медью, зная, что сплавив его с 3 кг чистого серебра, получают сплав 900–й пробы, а сплавив его с 2 кг сплава 900–й пробы, получают сплав 840–й пробы. Решение: Пусть сплав содержит x кг серебра и у кг меди. Сплавив его с 3 кг чистого серебра, получим: x + 3 Получим систему уравнений: Теперь масса сплава: x + у – 2,4 + 0,6 = 3 кг, проба его равна: Ответ: 800–я проба. Задачи на комбинацию арифметической и геометрической прогрессий При решении этих задач используют формулы для нахождения общего члена прогрессий и их свойства.
Задача 16. Сумма трех чисел равна 27. Эти числа составляют арифметическую прогрессию. Если из каждого числа соответственно вычесть 1, 3 и 2, то они составят геометрическую прогрессию. Найти эти числа. Решение: Пусть числа x, у и z составляют арифметическую прогрессию, тогда Ответ: 13, 9, 5 или 4, 9, 14.
Задача 17. Четыре числа составляют геометрическую прогрессию. Если к каждому из них добавить соответственно 10, 11, 9 и 1, то новые числа составят арифметическую прогрессию. Решение: Пусть первый член геометрической прогрессии — x, а знаменатель — у. Тогда четыре члена геометрической прогрессии будут выглядеть так: x, xy, xy2 и xy3. Если к этим числам прибавить 10, 11, 9 и 1 соответственно, получим x + 10; xy + 11; xy2 + 9; xy3 + 1, это уже арифметическая прогрессия. Разделим первое уравнение почленно на второе, учитывая, что x – 0 и у – 1 не являются решениями системы: Тогда имеем 4 члена геометрической прогрессии: 2; 2 • 3; 2 • 32; 2 • 33, т. е. 2; 6; 12; 24. Ответ: 2; 6; 12; 24.
Задачи, в которых используется формула двузначного числа Задача 18. Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получим число, записанное теми же цифрами, но в обратном порядке. Найти это число. Решение: Пусть число имеет x десятков и у единиц. Тогда искомое число имеет вид 10x + у. Из условия задачи следует, что x2 + у2 = 13 и 10x + у – 9 = 10у + x или 9x – 9у = = 9, т. е. x – у – 1. Получим систему: Решив эту систему способом подстановки, получаем x – 3, у – 2. Ответ: 32.
Задачи, компонентами которых являются геометрические величины Задача 19. Сумма диагоналей ромба 34 см, а его сторона ромба. Решение: Решив систему способом подстановки, получим: x – 5, у – 12. Диагонали ромба 10 см и 24 см. Площадь ромба равна половине произведения диагоналей S – Ответ: 60 см2.
Задача 20. Две силы приложены к одной точке и направлены под прямым углом. Величина одной из них на 4 Н больше другой, а величина равнодействующей силы на 8 Н меньше суммы величин данных сил. Найти величины данных сил и их равнодействующей. Решение: Ответ: 12 Н, 16 Н, 20 Н.